Wandel und Fortschritt in der Mathematik
M. Atiyah • Michael F. Atiyah 1969 zum Thema: (Last Update: 01.01.2014)
Der Mathematiker veröffentlicht die Ergebnisse seiner Forschungen in
Fachzeitschriften. In diesen wissenschaftlichen Arbeiten werden
Theoreme bewiesen, die vorher nicht bekannt waren. Für einen
Laien scheint die mathematische Literatur erstaunlich umfangreich zu
sein, glaubt er manchmal doch sogar, es gäbe in der Mathematik
überhaupt nichts Neues mehr zu erforschen.
In den Mathematical Reviews, die in den USA erscheinen, werden alle in
der Welt veröffentlichten mathematischen Arbeiten besprochen. 1m
Jahre 1967 wurden 17141 Titel aufgenommen. Wieso gibt es so viele
ungelöste Probleme? Um was geht es in der heutigen Mathematik?
Für
einen Mathematiker, der bisher nur in Fachzeitschriften über
seine Forschungsergebnisse geschrieben hat, ist es eine ungewohnte
Aufgabe, sich an einen größeren Kreis zu wenden, der
hauptsächlich aus Nichtmathematikern besteht. Sicher werden
unter den Lesern viele sein, die in ihrem Beruf gelegentlich oder
auch fast täglich Teilgebieten der Mathematik begegnen. Dieser
Kontakt mit der Mathematik ist in den einzelnen Fächern
verschieden intensiv und auch sehr verschiedenartig. Alle stellen
jedoch fest, daß ein breiter Graben liegt zwischen der
Mathematik, wie sie dem wissenschaftlich arbeitenden
Nichtmathematiker begegnet, und der Mathematik, wie sie von den
reinen Mathematikern studiert wird.
Aus
diesem Grunde scheint ein Versuch der Mühe wert, in
allgemeinverständlichen Worten einen Überblick zu geben, um
was es sich bei der heutigen Mathematik handelt, wie sie sich aus der
Mathematik der Vergangenheit entwickelt hat und in welcher Beziehung
sie zum wissenschaftlichen Leben im allgemeinen steht. Dies sind
natürlich weitgespannte Fragen, weshalb es vermessen wäre,
sie in einem kurzen Artikel erschöpfend behandeln zu wollen.
Daher möge man verzeihen, daß hier zugunsten eines
einheitlichen Gesichtspunktes ein Leitgedanke ausgewählt wird,
obwohl es ohne Zweifel auch viele andere Blickwinkel gibt, unter
denen eine Betrachtung ebensogut denkbar und vertretbar wäre.
Ich will zufrieden sein, wenn ich Nichtmathematikern bis zu einem
gewissen Grade eine Idee vom Inhalt der modernen Mathematik
vermitteln kann. Es ist nicht zu erwarten, daß alle meine
mathematischen Kollegen, sofern sie diese Zeilen lesen, mit der
Auswahl dieser These einverstanden sind. Vielleicht werden sie jedoch
zum Nachdenken über diese These und die damit zusammenhängenden
allgemeinen Fragen angeregt.
Die
These, die ich vorschlagen mochte, lautet: Die Entwicklung der
Mathematik kann am besten als eine natürliche Reaktion auf die
wachsende Schwierigkeit und Komplexität der Probleme verstanden
werden, mit denen sie sich befassen muß. Soweit diese Probleme,
direkt oder indirekt, ihren Ursprung in den Naturwissenschaften oder
anderen Wissenschaften haben, spiegelt diese Komplexität an sich
schon die zunehmende Kompliziertheit und Differenziertheit der
modernen Wissenschaften wider.
Wir
wollen mit einer Betrachtung der frühen Entwicklungsstufe der
Mathematik beginnen, etwa in dem Jahrhundert vor Newton, der 1643
geboren wurde. Man kann sagen, daß damals das typische Problem
darin bestand, eine Zahl, den Wert einer unbekannten Größe,
zu finden, wenn bestimmte, diese Zahl betreffende Daten oder
Gleichungen gegeben waren. Im wesentlichen waren irgendwelche
einfachen algebraischen Gleichungen aufzustellen und zu lösen,
im einfachsten Fall 204 eine Gleichung ersten Grades wie
3x
- 6 = 0
aus
der man den Wert der Unbekannten x berechnen kann, nämlich x =
2, oder eine Gleichung zweiten Grades wie
x2
- 5x + 6 = 0
aus
der folgt, daß die Unbekannte x gleich 2 oder gleich 3 ist.
Die
Mathematiker jener Tage beschäftigten sich mit der Lösung
von Gleichungen höheren Grades, und tatsächlich ist die
Geschichte der Mathematik jener Zeit zum großen Teil die
Geschichte der Gleichungen dritten und vierten Grades.
Aber
die einzelne unbekannte Größe oder Variable war
begrifflich und mathematisch ganz unzureichend für die
Naturwissenschaft des 17. Jahrhunderts. Was gebraucht wurde, war der
Begriff einer Funktion. Eine Funktion ist ein Gesetz der
Abhängigkeit einer Variablen von einer anderen Variablen, wie
etwa bei einem sich bewegenden Gegenstand die Abhängigkeit des
zurückgelegten Weges von der Zeit. In der Tat läuft das
Auffinden einer unbekannten Funktion im wesentlichen darauf hinaus,
eine unendliche Zahl von Werten einer unbekannten Variablen zu
finden. Hierum bemühen sich alle Naturwissenschaftler, wenn sie
aus vielen einzelnen Ablesungen eine Kurve zusammenstellen.
Denken
wir an das Fallgesetz (Galilei, 1564-1642). Nach einer Fallzeit von t
Sekunden hat ein frei fallender Körper - bei Vernachlässigung
des Luftwiderstandes - den Weg von 4,9 * t2 Metern
zurückgelegt. Ordnet man jeder Zahl t den 2 Wert 4,9 * t2
zu, dann erhält man eine Funktion, hier das Gesetz der
Abhängigkeit des zurückgelegten Weges von der Zeit beim
freien Fall. Diese Zuordnungsvorschrift heiße f. Der f
zugeordnete Wert wird f(t) genannt.
f(t)
= 4,9 * t2
Den
zurückgelegten Weg kann man nur für einzelne Werte von t
messen. Mit Hilfe vieler Messungen kann man das Gesetz erraten. Die
Funktion f ermöglicht die Berechnung des zurückgelegten
Weges für jeden Wert von t.
Das
Neue am mathematischen Begriff der Funktion war, sie - in unserem
Beispiel also die Funktion f - als ein einziges mathematisches Objekt
anzusehen. Seine Einführung war ein entscheidender Schritt
vorwärts und befähigte die Mathematiker, die
komplizierteren Fragen zu behandeln, die durch die Anfänge der
modernen naturwissenschaftlichen Forschung aufgeworfen wurden.
In
der zweiten Hälfte des 17. Jahrhunderts entstand die
Differential- und Integralrechnung, im wesentlichen durch die Arbeit
von Newton und Leibniz. Von dieser Zeit bis in das 19. Jahrhundert
war das typische mathematische Problem, eine unbekannte Funktion zu
finden, wenn bestimmte, diese Funktion betreffende Daten und
Gleichungen gegeben waren. Diese Gleichungen wurden gewöhnlich
mit Hilfe von Ausdrücken der Differential- und Integralrechnung
formuliert. So wurde das Studium von Differential- und
Integralgleichungen entscheidend für den Fortschritt der
physikalischen Wissenschaften. Die Theorie der Funktionen wurde zum
Hauptanliegen der Mathematiker. Wir können hier keine Beispiele
von komplizierten Differential- und Integralgleichungen geben. Die
meisten Leser werden jedoch die Ableitung f ' einer Funktion f von
der Schule her kennen. f ' ist selbst wieder eine Funktion. Für
die vorhin erwähnte Funktion f mit
f(t)
= 4,9 * t2
ist
f ' die Funktion, die zur Zeit t den Wert 9,8 * t hat.
f
' (t) = 9,8 * t
f
' (t) ist die Geschwindigkeit in Meter pro Sekunde, die
der frei fallende Körper nach t Sekunden hat. Die
Berechnung von f ',
wenn f bekannt ist,
oder die Berechnung von f, wenn f ' bekannt ist, sind die
Grundaufgaben der Differential- und Integralrechnung. Was bisher
gesagt wurde, ist natürlich allgemein bekannt. Es sollte damit
nur eine gewisse historische Perspektive gegeben werden. Wir wollen
jetzt die Mathematik der letzten hundert Jahre unter dem Licht der
aufgestellten These betrachten.
Was
ist an die Stelle der Theorie der Funktionen und der Untersuchung von
Funktionen mit Hilfe von Differential- und Integralgleichungen
getreten? Warum spielen heute andere Gebiete der Mathematik eine
ähnlich fundamentale Rolle wie früher die Theorie der
Funktionen?
Um
zu verstehen, was geschehen ist, sollten wir den Standpunkt des
Mathematikers einnehmen. Seine Aufgabe bestand darin, Funktionen zu
studieren. Aber mit der Zeit traten mehr und mehr Typen von
Funktionen auf, praktischen oder theoretischen Ursprungs, und sie
wurden immer komplizierter. Insbesondere mußte der Mathematiker
statt einer Funktion einer Variablen oft viele Funktionen vieler
Variablen und sie verbindende Differential- und Integralgleichungen
betrachten. Denken wir etwa an die Hydrodynamik, wo sich bewegende,
räumlich ausgedehnte Flüssigkeiten oder Gase behandelt
werden. Druck, Dichte und die drei Geschwindigkeitskomponenten sind
abhängig von Ort und Zeit. Da der Ort durch drei Raumkoordinaten
gegeben wird, erhält man als Beispiel ein System von fünf
Funktionen von vier Veränderlichen.
Vom
theoretischen Standpunkt aus bestand die Aufgabe des Mathematikers
offensichtlich darin, etwas Ordnung in dieses Chaos zu bringen. Er
mußte neue Methoden ersinnen, um mit dieser immer größer
werdenden Komplexität fertig zu werden. Was konnte er tun?
Ich
mochte auf drei verschiedene Entwicklungen in der modernen Mathematik
hinweisen, die, wie ich glaube, durch dieses Problem der
fortschreitenden Komplexität motiviert wurden und die darauf
Teilantworten geliefert haben. Sicher gibt es auch noch andere
Entwicklungsrichtungen in der Mathematik, die man in ähnlicher
Weise betrachten konnte.
Die
erste und vielleicht am einfachsten zu erklärende Methode ist
die konsequente Ausnutzung der symmetrischen Eigenschaften, die eine
vorgegebene mathematische Problemstellung hat. Jeder hat eine
intuitive Vorstellung davon, was Symmetrie bedeutet. Symmetrie
kann natürlich in ganz verschiedenen Zusammenhängen
vorkommen. Sie kann bei physikalischen und mathematischen, bei
geometrischen und algebraischen Sachverhalten vorhanden sein. Zum
Beispiel sind
x2+y2+z2
und
xy
+ zt
algebraische
Ausdrücke mit Symmetrieeigenschaften. In dem ersten Ausdruck ist
die Symmetrie vollständig, die drei Variablen spielen identische
Rollen, bei einer beliebigen Permutation (Vertauschung) von x, y
und z - es gibt insgesamt 6 - geht der algebraische Ausdruck
x2+y2+z2 in sich über.
Im zweiten Fall handelt es sich nur um eine Teilsymmetrie. Zum
Beispiel läßt die Permutation, welche x in x, y in
z, z in y und t in t überführt, den algebraischen
Ausdruck nicht unverändert. Es gibt insgesamt 24 verschiedene
Permutationen von x, y, z, t. Man kann leicht feststellen, daß
davon genau die folgenden 8 Permutationen den Ausdruck xy + zt
unverändert lassen. (Die Regeln a+b = b+a und
ab = ba dürfen verwandt werden.)
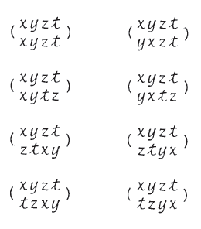
Dabei
bedeutet zum Beispiel die letztgenannte Permutation, daß x in
t, y in z, z in y und t in x überführt wird.
Unter
einer Bewegung versteht man eine Abbildung der Ebene bzw. des Raumes
auf sich, die zwei beliebige Punkte stets in zwei Punkte gleichen
Abstands überführt. Zwei ebene bzw. räumliche
geometrische Figuren heißen kongruent, wenn sich eine Bewegung
ausführen läßt, mit der die eine Figur in die andere
überführt werden kann. Die Gesamtheit aller Bewegungen, die
eine geometrische Figur in sieh überführen, also die
Gesamtheit der Selbstkongruenzen der Figur, nennt man die
Symmetriegruppe der Figur. Im Falle des gleichseitigen Dreiecks, des
Quadrats und des regulären Fünfecks müssen aIle
Bewegungen, die zur Symmetriegruppe gehören, den Mittelpunkt
festlassen und die Eckpunkte permutieren. Durch die Vertauschung der
Eckpunkte ist die Bewegung bereits festgelegt, im Falle des
gleichseitigen Dreiecks kommen alle 6 Vertauschungen der Eckpunkte
vor, im Falle des Quadrats von den 24 möglichen Vertauschungen
nur 8 Vertauschungen, nämlich die zyklischen Vertauschungen, die
sieh aus den Drehungen um 0, 90, 180 und 270 Grad ergeben, und die 4
Vertauschungen, die den Spiegelungen an den 4 Symmetrieachsen
entsprechen.

Für
die Kugel besteht die Symmetriegruppe aus allen Bewegungen des
Raumes, die den Mittelpunkt der Kugel festlassen. Dazu gehören
insbesondere alle Drehungen um irgendeinen Drehwinkel um eine
beliebige durch den Mittelpunkt gehende Achse. Zwei Punkte des Raumes
lassen sich durch eine Bewegung, die zu dieser Symmetriegruppe
gehört, genau dann ineinander überführen, wenn sie vom
Mittelpunkt M der Kugel den gleichen Abstand haben. Ist ein Problem
kugelsymmetrisch, dann wird deshalb der Abstand vom Mittelpunkt die
entscheidende Größe sein.
Wie
sicher einleuchtend ist, wird ein Problem sehr vereinfacht, wenn man
vor Beginn der Untersuchung weiß, daß das Problem einen
bestimmten Symmetrietyp hat. Hierdurch kann häufig die Anzahl
unbekannter Variablen oder Funktionen drastisch reduziert werden. Das
gerade diskutierte Beispiel der Kugelsymmetrie kommt im Zusammenhang
mit elektrischen Ladungen vor: Wenn man die Feldstärke an einer
Stelle P, verursacht durch eine Ladung im Punkt M, untersucht, beruft
man sich auf die Kugelsymmetrie (Mittelpunkt M) und schließt,
daß die Feldstärke eine Funktion der Entfernung von P
und M sein muß.
Diese
wenigen Bemerkungen deuten bereits darauf hin, daß ein
mathematisches Studium der Symmetrie von großem Nutzen sein
müßte, um Ordnung in komplizierte Situationen zu bringen.
Außerdem möchte man eine einzige abstrakte Theorie der
Symmetrie haben, die alle die verschiedenen geometrischen und
algebraischen Fälle der Symmetrie erfaßt. Daß eine
solche Zusammenfassung möglich sein könnte, wird durch
Beispiele motiviert.
So
hat etwa der algebraische Ausdruck
x2+y2+z2
vom Standpunkt der Symmetrie aus mehr mit einem gleichseitigen
Dreieck, also mit einer geometrischen Figur, gemein als mit dem
algebraischen Ausdruck xy+zt.
In
x2+y2+z2
bzw. in dem gleichseitigen Dreieck können die drei Variablen
x,y,z bzw. die
drei Eckpunkte beliebig vertauscht werden.
Mit
anderen Worten, Symmetrie hat mehr mit den Wechselbeziehungen der
Objekte untereinander zu tun als mit ihrer Natur. Eine geometrische
Figur und ein algebraischer Ausdruck können also dieselbe Art
von Symmetrie haben. Der algebraische Ausdruck xy+zt und das
Quadrat lassen übrigens ebenfalls Symmetriegruppen gleicher Art
zu. Wir bezeichnen die Eckpunkte des Quadrats wie folgt:

und
sehen dann. daß es sich in beiden Fällen um dieselben 8
Vertauschungen der 4 Symbole x, y,
z, t
handelt, die vorher aufgezeigt wurden.
Das
Studium der abstrakten Symmetrie hat sich schon seit den Resultaten
von Galois (1811-1832) über die Permutation der Wurzeln einer
algebraischen Gleichung stark entwickelt. Es wird als
'Gruppentheorie' bezeichnet und ist jetzt eines der zentralen
Gebiete der Mathematik.
Eine
Gruppe wird axiomatisch durch Eigenschaften definiert, die bei einer
Symmetriegruppe offensichtlich erfüllt sind. Eine Gruppe G ist
eine Menge von irgendwelchen abstrakten Objekten, für die eine
Verknüpfung definiert ist, d.h. für Objekte a, b der
Gruppe G ist ein Objekt aob
der Gruppe erklärt. Für eine Symmetriegruppe (denken
wir etwa an die Selbstkongruenzen einer geometrischen Figur) ist aob
die Selbstkongruenz, die man erhält, wenn man erst die
Selbstkongruenz b und danach die Selbstkongruenz a
ausführt. So konnte etwa beim Quadrat b die Drehung
um 90 Grad und a die Drehung um 180 Grad sein, aob ist
dann die Drehung um 270 Grad. Die Gruppenverknüpfung soll
gewisse Axiome erfüllen z.B. ao(boc) = (aob)oc, die,
wie gesagt, bei einer Symmetriegruppe offensichtlich richtig sind.
Die
Gruppentheorie ist typisch für den modernen Geist in der
Mathematik, und der Begriff einer Symmetriegruppe ist so grundlegend
für das 20. Jahrhundert, wie es der Begriff einer Funktion noch
für das 19. Jahrhundert war. Es ist nicht verwunderlich, daß
es zahlreiche wichtige Anwendungen der Gruppentheorie
(Symmetrietheorie) in der Kristallographie und der Quantenchemie
gibt. In allerletzter Zeit hat sie zu überraschenden neuen
Entwicklungen in der Physik der Elementarteilchen geführt. In
jedem Falle steht fest, daß sie einen Weg zeigt, um mit der
wachsenden Komplexität der mathematischen und physikalischen
Probleme fertig zu werden.
Eine
ganz andere Methode zur Behandlung komplizierter Probleme liegt im
Gebrauch der Wahrscheinlichkeit. Wenn die Zahl der unbekannten
Variablen sehr groß ist, gibt man den Versuch auf, das Problem
vollständig zu lösen, und begnügt sich mit einer
Antwort, durch die ein Maß der Wahrscheinlichkeit gegeben wird.
Natürlich
reicht die Wahrscheinlichkeitstheorie in ihren einfacheren Formen
weit zurück in die Geschichte der Mathematik, aber erst die
Anforderungen der Naturwissenschaften in den letzten hundert Jahren
machten sie schnell zu einem wichtigen Zweig der Mathematik. Zur Zeit
besitzt die Wahrscheinlichkeitstheorie eine abstrakte Form. Sie muß
in gleicher Weise für alle Fälle gelten, wo man es mit
einer großen Zahl von Objekten zu tun hat, ob diese Objekte nun
die Wiederholungen eines Experimentes (wie beim Würfeln) oder
die Moleküle eines Gases (wie in der Thermodynamik) oder die
Einzelpersonen einer Bevölkerung (wie in der Ökonomie)
sind. Die Theorie beschreibt also z.B. physikalische Erscheinungen
wie die Brownsche Bewegung der Moleküle und zufällige
Störungen im Funkverkehr, macht aber auch Aussagen über die
Wartezeiten von Flugzeugen vor der Landung auf einem Flugplatz, über
die günstigste Bestellstrategie für ein Warenlager und über
die Zuverlässigkeit eines aus vielen Einzelteilen
zusammengesetzten elektronischen Apparates.
In
allen diesen Fallen ist die Wahrscheinlichkeitsverteilung der
grundlegende Begriff, der die klassische Idee der Funktion ersetzt
hat. Da die Anwendungsmöglichkeiten und die Bedeutung der
Wahrscheinlichkeitstheorie im allgemeinen gut bekannt sind, soll
hierüber nicht mehr gesagt sein, sondern zu einer dritten,
weniger bekannten Entwicklung übergegangen werden.
Diesen
dritten großen Zweig der Mathematik, dessen Entstehung wir im
Licht der am Anfang aufgestellten These sehen wollen, konnte man
qualitative Mathematik nennen. Untersucht man eine Funktion,
ist man oft mehr an ihren allgemeinen Merkmalen als ihrem Verhalten
im einzelnen interessiert. Betrachten wir die graphischen
Darstellungen einiger Funktionen auf dieser Seite.

Die
ersten beiden Funktionen sind von der gleichen Art, die nächsten
zwei gehören zu einer anderen Art, die letzte zu einer dritten.
Als weiteres Beispiel untersuchen wir die Funktionen x2 +
ky2, wobei k eine von Null
verschiedene Konstante ist (d.h. die Funktionen, die dem Punkt der
Ebene mit den Koordinaten (x,
y) den
Wert x2
+ ky2
zuordnen). Alle diese
Funktionen mit positiver Konstante k
sind in gewissem Sinne
gleichartig, aber sie unterscheiden sich qualitativ von den
Funktionen, die sich ergeben, wenn k
negativ ist. Zur
Veranschaulichung stellen wir zwei dieser Funktionen in einem
räumlichen Koordinatensystem dar, und zwar einmal für
k = 1/5, und dann fur k = -1/5. Im ersten Fall hat man
im Punkte x = y = 0 ein Minimum, im anderen Fall einen
sogenannten Sattelpunkt.

Die
qualitative Mathematik untersucht die allgemeinen Merkmale der
Funktionen und ordnet nach Kriterien ein, die schön an so
einfachen Beispielen wie in der folgenden Abbildung deutlich werden:
die ersten beiden Funktionen sind von gleicher Art, die nächsten
zwei gehören zu einer anderen, die letzte zu einer dritten. Das
Beispiel oben zeigt Funktionen x2 + ky2.
Für verschiedene, aber positive Werte von Q erhält man
im Nullpunkt des Achsenkreuzes ein Minimum, für negative k
jedoch einen sogenannten Sattelpunkt. Je nach dem Vorzeichen von
Q resultieren also zwei verschiedene Arten. (...)


Ein
aufschlußreiches Beispiel der qualitativen Klassifikationen
bieten die Oberflächen einer Kugel, eines Ellipsoids, eines
Torus und einer Brezel. Die qualitativen Unterschiede zeigen sich zum
Beispiel im Verhalten einer strömenden Flüssigkeit auf
beiden Flächen. (Physikalische Erwägungen über die
Komprimierbarkeit werden außer acht gelassen.) Bei Kugel und
Ellipsoid gibt es immer wenigstens einen Stagnationspunkt. Der Torus
kann jedoch ohne Stagnationspunkt umflossen werden. Deshalb gehören
diese Flächen zu verschiedenen Typen. Bei der Brezeloberfläche
gibt es wie bei der Kugeloberfläche stets wenigstens einen
Stagnationspunkt, doch im Gegensatz zu dieser keine Strömung,
bei der nur Stagnationspunkte der Arten (1), (2), (3) auftreten.
Möglich ist eine Strömung mit zwei Stagnationspunkten der
Art (4), wie sie sich aus den Strömungsbildern (5) zweier mit
einem Loch versehener Torusflachen ergibt, wenn man diese längs
der Lochränder zur Brezel vereinigt.
Werden
die Fragen komplizierter, so ist es oft unrealistisch, eine genaue,
quantitative Antwort zu erwarten, und man begnügt sich daher
gern mit einer qualitativen Antwort, wie sie durch die obigen
einfachen Zeichnungen illustriert wird. Eine weitere qualitative
Eigenschaft einer Funktion besteht darin, ob sie periodisch ist oder
nicht: Gilt f(x+a) = f(x) für wenigstens ein a
und alle x, so nennt man die Funktion f periodisch. Geometrisch
entspricht dies dem Unterschied eines Kreises von einer unendlichen
Geraden.
Ein
etwas interessanteres Beispiel ist die Unterscheidung zwischen der
Oberfläche der Kugel, des Ellipsoids, des
fahrradschlauchähnlichen Torus und der Brezel (...). So zeigt
sich, daß die ersten beiden zum gleichen qualitativen Typ
gehören, wenn auch die betreffenden Konstanten (Achsenlängen)
verschiedene Werte haben. Die dritte und vierte sind andere Typen.
Es
mag überraschend erscheinen, daß es möglich ist,
solche qualitativen Begriffe mathematisch zu behandeln, aber es ist
tatsächlich möglich und bildet den Inhalt der Topologie,
eines der Hauptzweige der heutigen Mathematik. Man könnte etwa
sagen, daß es das Ziel der Topologie ist, Funktionen (oder
Konfigurationen oder andere mathematische Objekte) in Typen
einzuteilen oder zu klassifizieren und zu versuchen, die gemeinsamen
Merkmale aller Funktionen desselben Typs zu finden. Was unter dem Typ
einer Funktion zu verstehen ist, ändert sich natürlich
gemäß der Natur des Problems, aber die einfachen
Beispiele, die hier angeführt wurden, geben einen gewissen
Begriff davon, um was es sich handelt.
Angesichts
der Bedeutung, die in den Anfängen der Mathematik den Zahlen
beigemessen wurde, pflegt man es als selbstverständlich
anzusehen, daß die Mathematik unweigerlich quantitativ ist, und
die qualitative Seite, von der gerade gesprochen wurde, bedeutet für
manche Menschen eine gewisse Überraschung. Das entscheidende
Merkmal der Mathematik ist jedoch die Genauigkeit, und man kann bei
Klassifikationsproblemen ebenso genau sein wie bei Zahlenproblemen.
Man
muß zugeben, daß die Topologie bisher noch nicht viel
Anwendung in den Naturwissenschaften gefunden hat. Andererseits war
sie von ungeheurem Wert für Mathematiker aller Richtungen. Sie
hat in vielen verschiedenen Zweigen einen Rahmen zur Ordnung und
Systematisierung geliefert und uns zu einem tieferen Verständnis
verholfen. Indirekt und auf lange Sicht muß sich auch in der
praktischen Anwendung ihr Einfluß geltend machen.
So
sei noch erwähnt, daß der bedeutende französische
Mathematiker René Thorn diese qualitativen Begriffe zum Zwecke
ihrer Anwendung in der Biologie entwickelt hat. Er hat auch bereits
Vortrage darüber gehalten, und ein Buch wird in nächster
Zukunft erscheinen. Hier konnte der Beginn einer wichtigen
Entwicklung liegen.
Die
drei Zweige der Mathematik, die hier erwähnt wurden, nämlich
die Gruppentheorie, die Wahrscheinlichkeitslehre und
die Topologie, sind typische Hauptgebiete der modernen
Mathematik. Sie alle behandeln abstrakte Begriffe (Symmetrie,
Wahrscheinlichkeitsmaße, qualitative Klassifikationen), die
erheblich anspruchsvoller sind als die Begriffe Zahl und Funktion.
Diese Abstraktheit der modernen Mathematik wird oft kritisiert, und
ich muß zugeben, daß die Abstraktion teilweise zu weit
geht, aber ich wollte zeigen, daß sich die abstrakten Begriffe
als natürliche Antwort auf den Druck der Ereignisse ergaben.
Ohne
sie wäre die Mathematik jetzt schon von einer Menge
komplizierter Einzelheiten erdrückt und in unzählbare,
nicht miteinander verbundene Sonderfalle aufgespalten. Wir sehen
also, daß sich die Natur der Mathematik ändert. Neue
Begriffe, die vor hundert Jahren noch kaum bekannt waren, stehen
jetzt im Mittelpunkt. Dies bedeutet aber nicht, daß sich der
Grundgehalt der Mathematik völlig geändert hatte.
´
Wir
beschäftigen uns noch immer mit Zahlen und algebraischen
Gleichungen, mit Funktionen und Differentialgleichungen, aber wir
haben jetzt eine Vielfalt neuer Werkzeuge zu unserer Verfügung.
Wir
können Probleme in Angriff nehmen, die unsere Vorgänger als
hoffnungslos kompliziert angesehen hatten. Wir besitzen einen
größeren Überblick und können die
zugrundeliegenden Einheiten in der Mathematik erkennen, die früher
nur unklar wahrgenommen wurden.
(Aus: M. Atiyah,
»Wandel und Fortschritt in der Mathematik«, Stuttgart, 1969«)
Ihr Kommentar
Falls Sie Stellung nehmen, etwas ergänzen oder korrigieren möchten, können sie das hier gerne tun. Wir freuen uns über Ihre Nachricht.

